Los poderes visuales de Mondulio.
2. La visión de rayos X

Zonal / segundo nivel / 2007
Se tienen 20 tarjetas, cada una con un número entero distinto desde el 1 hasta el 20. Hay que formar 9 grupos de tarjetas de modo que en cada grupo la multiplicación de los números de las tarjetas sea un cuadrado perfecto. Cada tarjeta se usa como mucho una vez y puede haber tarjetas que no se usan. Los grupos pueden tener una o más tarjetas cada uno, y si un grupo tiene una sola tarjeta el número de esa tarjeta tiene que ser un cuadrado perfecto.

¿Qué forma tienen los cuadrados perfectos? 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, ...
Con la visión rayos X (de factorización) Mondulio ve 1, 2x2, 3x3, 2x2x2x2, 5x5, 2x2x3x3, 7x7, 2x2x2x2x2x2, 3x3x3x3, 2x2x5x5, 11x11, 2x2x2x2x3x3, 13x13, 2x2x7x7. Se ve que todo factor primo aparece un número par de veces, ya que como son cuadrados perfectos los factores deberían poder partirse, y lo hacen, en dos conjuntos iguales.

Si hay que elegir algunos números de 1 a 20 para que se puedan agrupar en nueve conjuntos tales que multiplicadas den cuadrados perfectos.

Mondulio ve con su visión de rayos X los números: 1, 2, 3, 2x2, 5, 2x3, 7, 2x2x2, 3x3, 2x5, 11, 2x2x3, 13, 2x7, 3x5, 2x2x2x2, 17, 2x3x3, 19, 2x2x5.

Decide entonces tomar acciones.
1. Tomar 1, 4, 9 y 16 que son por sí mismos cuadrados perfectos.
2. Descartar los números 11, 13, 17 y 19 que no tienen otro factor igual entre los números de 1 a 20 lo que no permite formar cuadrados perfectos.

Quedan por agrupar 2, 3, 5, 2x3, 7, 2x2x2, 2x5, 2x2x3, 2x7, 3x5, 2x3x3, 2x2x5. para formar los cinco cuadrados perfectos que faltan.

5 y 2x2x5 o sea 5 y 20 forman el 100 que es CP
2 y 2x3x3 o sea 2 y 18 forman el 36 que es CP
3 y 2x2x3 o sea 3 y 12 forman el 36 que es CP

Quedan finalmente 2x3, 7, 2x2x2, 2x5, 2x7, 3x5 que no se pueden agrupar de a pares pero si de a trios.
El 7 tiene que aparearse con el 2x7 y para emparejar los 2 agregamos el 2x2x2 con lo cual se forma el trío 7, 8 y 14 que forma el cuadrado perfecto 784 = 28x28.
Finalmente queda el trío 2x3, 2x5 y 3x5 o sea 6,10 y 15 que forman el cuadrado perfecto 900 = 30x30.

Los poderes visuales de Mondulio
1. La visión infrarroja

Regional / primer nivel / 1995
Escribir en cada vértice de un cuadrado una potencia de 2 y luego, en cada lado y en cada diagonal escribir el producto de los números asignados a sus extremos, de modo tal que la suma de los 10 números escritos sea 3505. ACLARACION: Las potencias de 2 son 2^0=1, 2^1=2, 2^2=4, ...


La habilidad visual que es útil para este problema es la de ver los números como sumas de potencias de dos. Esto no es otra cosa que ver los números en base 2.
¿Cómo se ve 3505 en base 2? Se lo va dividiendo por 2 y se van tomando los restos de las sucesivas divisiones como dígitos de la representación de 3505 en base 2.


2^X --- 2^Y
\ /
\ /
\/
/\
/ \
/ \
2^Z --- 2^W



2^X-2^X+Y-2^Y
\ /
2^X+W /
2^X+Z \/ 2^Y+W
/\
2^Y+Z \
/ \
2^Z-2^Z+W-2^W


como 3505 es impar entonces uno de los exponentes W,X,Y,Z debe ser cero. Supongamos que sea W=0.

2^X -2^X+Y-2^Y
\ /
2^X /
2^X+Z \/ 2^Y
/\
2^Y+Z \
/ \
2^Z - 2^Z--1


La suma total termina siendo 2^(X+Y)+2^(X+Z)+2^(Y+Z)+2^(X+1)+2^(Y+1)+2^(Z+1)+1
Como el desarrollo de 3505 en base 2 es 110110110001 = 2^11+2^10+2^8+2^7+2^5+2^4+2^0


Podemos suponer sin "perder generalidad" que X>Y>Z entonces de ahí deducimos que Z = 3, Y = 4 por ser 2^4 y 2^5 las potencias menores de 2 fuera de 2^0 presentes en el desarrollo binario de 3505. Nos queda entonces que 2^7 es 2^(Y+Z), con lo cual X = 7 por ser 2^(X+1) = 2^8 la potencia de dos más chica sin definir.

Finalmente 2^(X+Z) = 2^(7+3) = 2^10 y 2^(X+Y) = 2^(7+4) = 2^11 que son las dos potencias del desarrollo binario de 3505 que me faltaba definir.

¿Qué hace que las personas sean personales?
Respuesta: las experincias vividas.
Si yo escuché una balalaica o uso habitualmente sobretodos o como queso Romadur, tengo vicencias diferentes a quienes nunca tuvieron esas experiencias y seguramente han tenido otras que yo no he tenido, como ver Bailando por un Sueño o haber escalado el Everest y eso los hace personales.La experiencia matemática, como todas las experiencias de la vida, contribuye también a hacer personales a las personas. La visión de los números enteros de una persona que ha tenido experiencia matemática (Mondulio) es diferente de una persona que no ha tenido esa suerte (Obdulio).
Cuando Mondulio ve un 12 ve además 2*2*3 o ve 2*2*2+2*2 o ve 1100 o ve 2*(2*(2+1))+0)+0 o ve un 000000000000 o ve un 5 modulo 7. En cambio cuando Obdulio ve un 12 ve simplemente un 12.En cierto sentido Mondulio es como los perros o los murciélagos que son capaces de percibir otros tipos de ondas que los humanos no pueden. O puede pensarse que su visión está enriquecida por instrumentos como visores infrarrojos que permiten ver en la oscuridad o visores de rayos X que ven a través de las paredes.

Sobre la regional que se viene...

Hola a todos! Les cuento que este año no los voy a poder acompañar a la regional porque voy a estar de viaje, y como además se vienen todos los feriados de septiembre, casi que no nos vamos a ver la cara por un largo tiempo... Les deseo mucha mucha suerte y les dejo a continuación problemas de la regional del 2004 para que practiquen!
Por favor no se olviden de llevar las autorizaciones ni bien puedan los que todavía no lo hicieron, y déjenlas en el departamento de matemática, o en rectoría para que las sellen.
De nuevo, mucha suerte! Nos vemos en la nacional ;)
Martín.

Regional 2004 (1er Nivel)

Estos son los problemas del Primer nivel

1

La ley pirata establece que para repartir las monedas de un tesoro el capitán debe elegir un grupo de piratas y repartir equitativamente las monedas entre los piratas elegidos hasta que no haya suficientes para darle una más a cada uno. Las monedas sobrantes son la parte del capitán. Morgan debe repartir un tesoro con menos de 1000 monedas de oro. El sabe que si elige 99 piratas se quedará con 51 monedas y si elige 77 piratas le corresponderán sólo 29 monedas.
Determinar cuántos piratas debe elegir Morgan para quedarse con la mayor cantidad de monedas respetando la ley pirata, y para esa cantidad de piratas, cuántas monedas le corresponden a Morgan.
ACLARACIÓN: Los piratas elegidos deben recibir por lo menos una moneda cada uno.

2

Nico debe elegir tres números enteros distintos entre 1 y 20 inclusive de modo que al multiplicar los tres números se obtenga un múltuplo de 4.
Calcular cuántas maneras tiene Nico de elegir sus tres números.
ACLARACIÓN: Dos elecciones que tienen los mismos tres números no importa en qué orden, son iguales.

3

En un trapecio ABCD de base mayor AB, base menor DC y lados no paralelos BC y DA, sea K el punto del lado BC tal que BK = 1/3 BC. Se traza por K la recta paralela a DA que corta a AB en L.
Si BL = CD y el área del trapecio ABCD es 20, calcular el área del triángulo ADL.

Regional 2004 (2do Nivel)

Estos son los problemas del Segundo Nivel

1

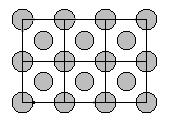
En un tablero cuadriculado de m x n se ubica una ficha en el centro de cada casilla y una ficha en cada vértice de la cuadrícula hasta que no quede lugar para más fichas (en la figura se muestra el tablero de 2 x 3 con sus 18 fichas).
Hallar las dimensiones m y n del tablero de m x n si se utilizan exactamente 500 fichas. Dar todas las posibilidades.

2

Fabio debe escribir una sucesión de números naturales.
El primer número lo elige Fabio entre 1 y 2004 inclusive, y a partir de alli, cada nuevo número se obtiene del anterior de acuerdo con la siguiente regla: si el anterior es impar, le suma 1, si el anterior es par, lo divide por 2. El proceso se detiene cuando se obtiene por primera vez el 1. Por ejemplo, si Fabio elige el primer número igual a 10, la sucesión será: 10, 5, 6, 3, 4, 2, 1, que tiene 7 números.
El objetivo de Fabio es lograr que su sucesión tenga la mayor cantidad posible de números. Determinar cuál es la máxima cantidad de números que puede tener la sucesión de Fabio y hallar un número inicial que le permita lograr una sucesión con esa cantidad máxima de números.

3

En el cuadrado ABCD de lado 6, sea M el punto medio del lado AD y N el punto medio del lado AB. La diagonal BD corta a CN en K y a CM en L.
Calcular el área del cuadrilátero KLMN.

Regional 2004 (3er Nivel)

Estos son los problemas del Tercer Nivel

1

Un programa de computadora genera una sucesión de 2004 números, de acuerdo con la siguiente regla: el primer número es 1, y a partir de allí, luego de generar el número x, el siguiente número que genera es igual a x + 1/[x].
Los primeros números de la sucesión son 1; 2; 5/2; 3; ... ; pues ...
Determinar cuál es el último número que genera el programa.
ACLARACIÓN: Los corchetes indican la parte entera del número.

2

Se suman las 102 potencias de 7 desde 7⁰ = 1 hasta 7¹⁰¹:

7⁰ + 7¹ + ... + 7¹⁰⁰ + 7¹⁰¹. Calcular el resto de dividir al resultado de esta suma por 400.

3

Dado un triángulo ABC rectángulo en C, con AC/BC = 3, sea O el punto medio de la hipotenusa AB.
Se traza por O la perpendicular a AB que corta al cateto AC en P; se traza por P la paralela a AB que corta al cateto BC en Q y se traza por Q la perpendicular a AB que corta a AB en R.
Calcular PQ/RQ

Problema "palito de la selva"

Hola a todos! Bueno, siguiendo la sugerencia de Fede vamos a instaurar los problemas "palito de la selva", que intentarán ser semanales pero vamos a ver cómo viene la mano...
Les dejo este que estuvimos haciendo un entrenamiento:
Sea ABC un triángulo de área 30. Se marcan los puntos M en el lado AC de forma tal que AM=2MC y N en el lado BC de forma tal que BN=NC. Si O es el punto de intersección de AN y BM, calcular el área del cuadrilátero CMON.
Bueno espero que les salga, cuenten sus soluciones! (por acá o en un entrenamiento!)

Problemita

Hola! Les dejo este problema que estuvimos viendo en el entrenamiento:
Sea ABC un triángulo tal que el ángulo B es el doble del ángulo C. Se traza la bisectriz del ángulo A que corta a BC en D. Si AB=CD, hallar los ángulos del triángulo ABC.
Espero que les salga! Cuenten sus soluciones!
Saludos y felices vacaciones,
Martín.

Sobre los entrenamientos en horas de clase

¡Hola a todos! Posteo por lo siguiente: en vistas a la regional, una ronda que es muy importante porque abre las puertas a la nacional y a las selecciones para las olimpíadas internacionales, resurge la idea de los entrenamientos para olimpíadas durante un 3er o 4to bloque por semana, que quizás vaya cambiando semana por medio para que no se pierda siempre la misma materia. La falta a ese bloque será eximida. Los requisitos para participar en estos entrenamientos son dos: haber clasificado para la regional, y quedarse también entrenando el mediodía que se asiste al entrenamiento en hora de clase. Aquellos que estén interesados, por favor, comenten este post dejando las materias que tienen en todos los terceros y cuartos bloques de lunes a viernes, su nombre y apellido y su año y división. También me pueden dar estos datos personalmente, en algún entrenamiento, o por mail.
Saludos a todos, ojalá esto se pueda armar y aumente nuestra preparación para los certámenes.
Martín.

Regional 2006 (1er nivel)

Hola a todos! Sigo publicando problemas, ahora los de la ronda que se viene para los que pasaron la zonal. Estos son los problemas del PRIMER NIVEL:

1. En el pizarrón están escritos los enteros positivos de 1 a 999, ordenados de izquierda a derecha en forma creciente. Se borran números mediante el siguiente procedimiento: En la primera etapa, comenzando de la izquierda, se deja un número y se borra el siguiente, hasta el final de la lista (se borran el 2, el 4, el 6, etc.). En la segunda etapa, comenzando de la derecha, se deja un número y se borra el siguiente, hasta el principio de la lista. En la tercera etapa, comenzando de la izquierda, se deja un número y se borra el siguiente, hasta el final de la lista. Y así siguiendo, en cada etapa se invierte el orden de la etapa anterior, y comenzando desde el extremo que corresponda se deja un número y se borra el siguiente una y otra vez hasta recorrer todos los números aun no borrados. El proceso se detiene cuando queda un solo número en el pizarrón. Determinar cuál es ese número.

2. En un programa de televisión compiten dos equipos A y B, realizando distintas pruebas. En cada prueba el ganador recibe siempre la misma cantidad de puntos, y el perdedor recibe una cantidad de puntos menor que el ganador, pero también es siempre la misma cantidad. Al cabo de varias pruebas, el equipo A tiene 231 puntos, y el equipo B, que ganó exactamente 3 pruebas tiene 176 puntos. Determinar cuántos puntos reciben el ganador y el perdedor de cada prueba.
ACLARACIÓN: La cantidad de puntos que recibe cada equipo en cada prueba es un entero positivo.

3. Dos hormigas caminan por los lados de un cuadrado de 35 cm de lado. Comienzan a moverse simultáneamente, desde el mismo vértice y en sentidos opuestos. Una hormiga va a 1 cm/seg y la otra a 2 cm/seg. Calcular la distancia (en línea recta) que separa a las hormigas cuando han transcurrido exactamente 817 segundos desde que salieron.

Regional 2006 (2do nivel)

Hola a todos! Sigo publicando problemas, ahora los de la ronda que se viene para los que pasaron la zonal. Estos son los problemas del SEGUNDO NIVEL:

1. En un colegio, el 81% de los alumnos estudia inglés y el 80% de los alumnos estudia computación. La proporción de los alumnos que estudian inglés entre los que estudian computación es igual al doble de la proporción de los alumnos que estudian inglés entre los que no estudian computación. Hallar el porcentaje de alumnos de la escuela que no estudia ni inglés ni computación.

2. La profesora escribe en el pizarrón una fila de dígitos 8 y le pide a un alumno que intercale algunos signos + para que la suma que quede indicada tenga resultado 1000. Dar todas las posibilidades para la cantidad de dígitos 8 que debe escribir la profesora para que la tarea del alumno tenga solución.

3. En el triángulo ABC, sea P un punto interior. La recta AP corta al lado BC en D, la recta BP corta al lado AC en E y la recta CP corta al lado AB en F. Se sabe que área (APF) =168; área(BPD)=80; área (CPD) = 60 y área (CPE) = 70.
Calcular el área del triángulo APE y el área del triángulo BPF.

Regional 2006 (3er nivel)

Hola a todos! Sigo publicando problemas, ahora los de la ronda que se viene para los que pasaron la zonal. Estos son los problemas del TERCER NIVEL:

1. Hallar todos los pares de números enteros M y N que verifican simultáneamente las siguientes condiciones:

· M y N son números de cuatro dígitos.

· M y N son cuadrados perfectos.

· Si se resta ordenadamente a cada dígito de M el correspondiente dígito de N (el primero menos el primero, el segundo menos el segundo, etc.) entre los cuatro resultados obtenidos, exactamente dos son ceros y los otros dos son 1 ó –1 (pueden ser los dos 1, los dos –1 o un 1 y un –1).

2. Hallar el máximo número natural de 100 dígitos tal que al multiplicarlo por 7 se obtiene un número de 100 dígitos.

3. Sea AB una cuerda de longitud 6 de una circunferencia de centro O y radio 5. El cuadrado PQRS está inscripto en el sector OAB de modo tal que P está en el radio OA, Q está en el radio OB y R y S pertenecen al arco de circunferencia . Hallar el área del cuadrado PQRS.

Metropolitana

La olimpíada metropolitana es una competencia entre los alumnos de capital federal que sacaron 5 o más problemas entre la intercolegial y la zonal. Los alumnos de ORT I clasificados para esta ronda son Morillo, Tomchinsky, Frieder, Zylber, Litman, Libster, Alonso, Waisberg y Fumbarg Joelson. La prueba es el Jueves 30 de Agosto, y la premiación el Viernes 31. Por lo tanto, la fecha límite para traer las autorizaciones es el viernes 24 de Agosto.
Felicitaciones a todos los chicos que clasificaron!

A continuación les dejo, para que vayan entrenando, los problemas que se tomaron en la II Metropolitana, en el 2000.

primer nivel

1. En el pizarrón hay escritos dos números naturales de dos cifras. Nicolás multiplicó entre si los dos números del pizarrón y obtuvo un número de cuatro cifras, con la primera cifra de la izquierda igual a 2. Pedro sumó los dos números del pizarrón.

Si al número de Nicolás se le suprime la primera cifra de la izquierda, resulta un número de tres cifras, igual al número de Pedro. Determinar cuáles pueden ser los dos números del pizarrón. Dar todas las posibilidades.

2. Decidir si es posible colocar en las casillas de un tablero de ajedrez de Sxs las 16 piezas blancas y las 16 piezas negras de manera tal que para cada pieza, el número de sus,vecinas blancas sea igual al número de sus vecinas negras.

Si la respuesta es afirmativa, colocar las piezas. Si la respuesta es negativa, explicar porqué.

ACLARACION: Dos piezas son vecinas si las casillas que ocupan se tocan en un lado o en un vértice.

3. Sean ABCD un cuadrado de lados AB = BC = CD = DA = 12, E el punto medio de DA y F el punto medio de BC. Se trazan los segmentos EF, AC y BE, que dividen al cuadrado en seis regiones. Calcular el área de cada una de estas regiones.

segundo nivel

1. El camino entre el pueblo y el refugio en la montaña mide un número entero de kilómetros. Una mañana, tres grupos de andinistas salen del pueblo hacia el refugio. El primer día, el grupo A recorre la sexta parte del camino, el grupo B la mitad del camino, y el grupo C la cuarta parte del camino. Al día siguiente, el grupo A recorre 100 km, el grupo B recorre 10 km, el grupo C recorre 78 km, y nadie llega al refugio. Si el grupo B ha recorrido en total, más distancia que el A, pero menos que el C, determinar cuánto mide el camino desde el pueblo hasta el refugio.

2. En el cuadrado ABCD se marcan los puntos P, Q en el lado AB de manera tal que AP = PQ = QB, y se marcan los puntos R, S en el lado BC de manera tal que BR = RS = SC. Se trazan: la recta AR; la recta paralela a AR que pasa por S; la recta DP; la recta paralela a DP que pasa por Q. Estas cuatro rectas delimitan un cuadrado de área 490. Hallar la medida del lado del cuadrado ABCD.

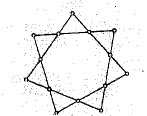
3. Asignar a cada uno de los puntos marcados en la figura uno de los números 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, sin repetir, de modo que en cada una de las 7 líneas la suma de los cuatro números asignados sea siempre la misma.

tercer nivel

1. Se escribe una lista de números de acuerdo con las siguientes reglas: en el primer paso se escribe 84; en el segundo paso se escribe 132. A partir de aquí, en cada paso se escribe el número que resulta de sumarle al último número escrito el máximo común divisor de los dos últimos números escritos. Por ejemplo, el tercer número es el resultado de 132+mcd(84;132).

¿En qué paso se escribirá por primera vez un número terminado en 7 ceros?

2. Matías debe elegir 1000 números enteros distintos entre 1 y 2000 inclusive, de modo tal que no haya entre los elegidos dos que sumen 2001, y que la suma de los 1000 números sea 1000500. Luego debe calcular la suma de los cuadrados de los 1000 números elegidos. ¿Cuántos resultados diferentes puede obtener?

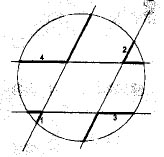
3. Un rombo está contenido en el interior de una circunferencia. Se prolongan cada uno de sus lados en los dos sentidos, hasta intersectar a la circunferencia; de este modo quedan determinados 8 segmentos con un vértice sobre la circunferencia y el otro coincidente con un vértice del rombo-. En la figura se indican las longitudes de cuatro de estos segmentos. Hallar la suma de las longitudes de los restantes cuatro segmentos.

Resultados Zonal

Hola a todos! Acá están los resultados de la zonal. Se pasa con 2 o más problemas bien, con la cantidad de menos que sea.
De 20 chicos que dieron la prueba pasaron a la regional 15. Felicitaciones!
Les recuerdo que la regional es el día 20 de Septiembre, por lo tanto la fecha límite para traer las autorizaciones es el viernes 14 de Septiembre.
Saludos,
Martín.

Aisemberg	1	0	0	1
Cukierman	1-	1	0	2-
Morillo	1	1	1	3
Barmaymon	1=	1	0	2=
Tomchinsky	1	1	0	2
Frieder	1	1	0	2
Zylber	1	1	0	2
Ochoa Ciro	1	0	0	1
Nozyce	1	1	1	3
Otero	1	1	0	2
Jawerbaum	0	0	0	0
Gold	1-	1	0	2-
Litman	1	1	1	3
Libster	1	1	0	2
Gartensztern	1	0	0	1
Gitlin	0	0	1=	1=
Alonso	1	1=	0	2=
Campos	1	1	0	2
Waisberg	1	1	0	2
Fumbarg Joelson	1	1	0	2

Zonal 2007 (segundo nivel)

Hola a todos! Este jueves fue el certamen Zonal. Les dejo los enunciados de los problemas de Segundo Nivel para que cuenten sus soluciones!

1. Se tienen dos recipientes, cada uno de ellos con 100 litros de capacidad. Inicialmente contienen entre los dos 100 litros de jugo. Se agrega jugo al primer recipiente hasta completar su capacidad. Luego se vierte jugo del primer recipiente al segundo hasta completar la capacidad del segundo. Finalmente, se vierten 12 litros del segundo recipiente en el primero. Así resulta que en el segundo recipiente hay 10 litros más de jugo que en el primero. Determinar cuánto jugo tenía inicialmente cada recipiente.

2. Se tienen 20 tarjetas, cada una con un número entero distinto desde el 1 hasta el 20. Hay que formar 9 grupos de tarjetas de modo que en cada grupo la multiplicación de los números de las tarjetas sea un cuadrado perfecto. Cada tarjeta se usa como mucho una vez y puede haber tarjetas que no se usan. Los grupos pueden tener una o más tarjetas cada uno, y si un grupo tiene una sola tarjeta el número de esa tarjeta tiene que ser un cuadrado perfecto.

3. Sea ABCD un cuadrado de papel de lados AB=BC=CD=DA=1O. El cuadrado se dobla a lo largo de una línea recta, haciendo coincidir el vértice A con el punto medio del lado BC. Esta línea recta corta al lado AB en E y al lado CD en F. Calcular la medida de EF.

Zonal 2007 (primer nivel)

Hola a todos! Este jueves fue el certamen Zonal. Les dejo los enunciados de los problemas de Primer Nivel para que cuenten sus soluciones!

1. Se tienen 100 tarjetas, cada una con un número entero distinto desde el 1 hasta el 100. Hay que formar grupos de tres tarjetas cada uno de modo que en cada grupo el número de una de las tarjetas sea igual a la multiplicación de los números de las otras dos. Por ejemplo, se podría formar el grupo 3, 31, 93, porque 93=3·31. Cada tarjeta se usa como mucho una vez y puede haber tarjetas que no se usan.

Formar la mayor cantidad posible de estos grupos y justificar por qué es imposible formar más.

2. En un barco pirata hay un cofre con monedas de oro. Cinco de los piratas reciben su parte con el siguiente procedimiento: primero Abel recibe 1/8 del total; luego Beto recibe 1/6 de lo que queda en el cofre. Más tarde, Carlos recibe 1/7 de lo que quedaba después de que les dieran a los dos primeros. A continuación, Dany recibe 1/5 de lo que queda y finalmente a Eze le dan 1/4 de lo que resta.

Hay tres piratas que recibieron igual cantidad de monedas. Determinar cuáles son.

3. Sea ABC un triángulo con AB=13, BC=15 Y AC=9. Sea r la recta paralela a BC trazada por A. La bisectriz del ángulo ABC corta a r en E y la bisectriz del ángulo ACB corta r en F. Calcular la medida del segmento EF.

Olimpiadas de Computacion y Matematica

Hola, aprovecho el post para presentarme, soy Pablo Heiber, docente de entrenamiento para olimpiadas que tienen que ver con computacion. La razon principal de este post es comentarles la existencia (para los que no sabian) de una olimpiada de computacion y matematica ( http://oma.org.ar/nacional/cym/ ) en la que se requieren conocimientos de matematica para resolver problemas "ayudados" por la computadora (en general, cuando hay que probar muchos casos se requiere el uso de la maquina de alguna forma, aunque hacen falta conocimientos de matematica para ver cuales son esos casos o acotarlos de modo que la computadora pueda evaluarlos en un tiempo razonable). Para ver problemas de pruebas pasadas pueden consultar la pagina de OMA ( http://oma.org.ar/enunciados/#cym ).

En esta ocasion estamos tomando la prueba Colegial (interna de ORT), que es la primer ronda necesaria para participar de la olimpiada. Esta tiene caracter no presencial y consta de 3 problemas que pueden resolver como quieran, con o sin ayuda de la computadora. La forma en la que usan la computadora es libre, aunque saber programar en cualquier lenguaje (para esta ronda) o en uno de los lenguajes de programacion oficiales (para las subsiguientes) es lo que mas ayuda. Una planilla de calculo tambien puede ser util en algunos problemas.

La prueba consiste de 1 PDF con las instrucciones de entrega y los ejercicios a resolver de cada nivel. Para cualquier consulta y para pedir que les mande la prueba escribanme a pabloheiber@gmail.com. Hay tiempo para resolverla hasta el lunes proximo!

Suerte!

Suerte!

Zonal 2006 (3er nivel)

Hola a todos! Sigo publicando problemas, ahora los de la ronda que se viene para los que pasaron la intercolegial. Estos son los problemas del TERCER NIVEL:

1. Nacho escribió una progresión aritmética de primer término 101 y diferencia 2: 101, 103, 105, ...
Nico escribió una progresión aritmética de primer término 5 y diferencia 10: 5, 15, 25, ...
Las dos progresiones tienen la misma cantidad de términos y las dos progresiones tienen la misma suma. Determinar cuántos términos tiene cada progresión y cuánto vale la suma.

2. Si a, b son números tales que

calcular el producto ab.

3. Sea ABC un triángulo rectángulo con , y . Sean D y E puntos del lado BC tales que y . Calcular la medida del ángulo

Zonal 2006 (2do nivel)

Hola a todos! Sigo publicando problemas, ahora los de la ronda que se viene para los que pasaron la intercolegial. Estos son los problemas del SEGUNDO NIVEL:

1. Hallar los seis números que se deben escribir en cada una de las seis casillas vacías para obtener un cuadrado mágico: las tres filas, las tres columnas y las dos diagonales tienen la misma suma.

2. Ana, Beto, Ceci, Dany y Eva tienen entre los cinco 80 monedas de un peso. La cantidad de monedas que tienen en conjunto Beto y Dany es igual a la quinta parte de las que tienen, en conjunto, Ana y Ceci. La cantidad de monedas que tienen en conjunto Ceci y Dany es igual a 6 veces las que tienen, en conjunto, Ana y Beto. Determinar cuántas monedas tiene cada uno si se sabe que Beto tiene 2 monedas más que Ana.

3. Sean P y Q puntos del plano tales que . La circunferencia de centro Q y radio 25 corta al segmento PQ en A.
La recta perpendicular a PQ trazada por A corta a la circunferencia de centro P y radio 41 en los puntos B y C.
Calcular la medida del segmento BC.

Zonal 2006 (1er nivel)

Hola a todos! Sigo publicando problemas, ahora los de la ronda que se viene para los que pasaron la intercolegial. Estos son los problemas del PRIMER NIVEL:

1. En el pizarrón se escriben los números enteros positivos impares desde 1 hasta 47, uno a continuación del otro, sin espacios intermedios. Queda así una larga secuencia de 43 dígitos (el primero es 1 y el último es 7):

135791113...4547.

Hay que borrar 33 dígitos de modo que los 10 dígitos que queden escritos, leídos de izquierda a derecha, formen el mayor número de 10 dígitos posible.
Determinar cuál es el número de 10 dígitos que quedará escrito en el pizarrón.

2. Un auto viaja de A a B a velocidad constante. A las 8 de la mañana ha recorrido exactamente la tercera parte del camino entre A y B, y a las 12 del mediodía lleva recorrido, en total, las partes del camino entre A y B. Determinar a qué hora ha recorrido exactamente la mitad del camino entre A y B.

3. Se tiene un triángulo ABC y un punto interior P tal que , y .
Calcular los ángulos del triángulo ABC.

Resultados Intercolegial

Hola a todos! Acá están los resultados de la intercolegial. En primer nivel se pasa con 1,5 o más, en segundo y tercer nivel con 2 o más.
De 26 chicos que participaron pasaron a la zonal 22. Felicitaciones!
Les recuerdo que la zonal es el día 5 de Julio, por lo tanto la fecha límite para traer las autorizaciones es el viernes 29 de Junio.
Saludos,
Martín.

Rosenberg	1	0	0	1
Aisemberg	1	1	0	2
Cukierman	1	1	1/2	2,5
Morillo	1	1	1	3
Barmaymon	0	1	1/2	1,5
Campana	0	0	0	0
Mosse	1	1	1	3
Bursztyn	1-	0	0	1-
Tomchinsky	1	1	1	3
Frieder	1	1	1	3
Zylber	1	1	1	3
Ochoa Ciro	1	1	0	2
Nozyce	1	1	1/2	2,5
Otero	1	1/2	0	1,5
Sigaloff	ausente
Jawerbaum	1	1	1	3
Gold	1	1	0	2
Litman	1	1	1	3
Libster	1	1	1	3
Gartensztern	1	1	1	3
Gitlin	1	1	0	2
Alonso	1	1	1	3
Andina	1	0	0	1
Campos	1	1	0	2
Eisenschlos	1	1-	1	3-
Waisberg	1	1	1	3
Fumbarg Joelson	1	1	1	3

Intercolegial 2006 (3er nivel)

Para empezar a entrenar con algo sencillo, publico los problemas de la intercolegial (es la primera ronda de las olimpíadas) del año pasado. Estos son los problemas del Tercer nivel (6to BTO)

TERCER NIVEL

1. En el pizarrón están escritos los números enteros desde 1 hasta 2006. Nacho borra números con el siguiente procedimiento: Recorre los números del pizarrón ordenadamente de menor a mayor comenzando con el 3. Borra el 3 y cada vez que llega a un número que se puede escribir
como suma de dos números distintos que no se hayan borrado hasta ese momento, lo borra. Determinar cuántos números quedarán en el pizarrón cuando Nacho concluya su tarea.

2. En un parque sólo hay gatos de dos colores: completamente blancos y completamente negros. Algunos son machos y los otros, hembras.
Los machos son el 55% del total de los gatos del parque.
La proporción entre machos blancos y machos negros es igual a la proporción entre gatos blancos y gatos negros.

Hallar la proporción entre machos blancos y hembras blancas.

3. Sea ABC un triángulo rectángulo e isósceles de hipotenusa BC. Consideramos los puntos D en el cateto AB y E en el cateto AC tales que

y . La paralela a AC por D corta a BC en G, y la paralela a AB por E corta a BC en F.

Si el área del trapecio DEFG es igual a 10, calcular la longitud de los catetos del triángulo ABC.

Intercolegial 2006 (2do nivel)

Para empezar a entrenar con algo sencillo, publico los problemas de la intercolegial (es la primera ronda de las olimpíadas) del año pasado. Estos son los problemas del Segundo nivel (4to y 5to BTO)

SEGUNDO NIVEL

1. En la tabla de la figura x, y, z representan números enteros. La suma de los cuatro números de la primera fila es igual a 78; la suma de los cuatro números de la cuarta fila es igual a 102 y la suma de los cuatro números de la segunda columna es igual a 81. (Tal como se indica en la figura.)
Hallar la suma de los 16 números de la tabla.

2. Un pequeño avión tarda 7 horas más que otro en ir de A a B. Las velocidades de los dos aviones son 660 km/h y 275 km/h. Calcular la

distancia entre A y B.

3. Sea ABC un triángulo rectángulo con

, y . Se traza por B la perpendicular a AC, que corta a AC en D. Sea E en el lado AC tal que .

Se traza por E la perpendicular a AC que corta a AB en F. Calcular la medida del segmento EF.